SHORT ANSWER: 0 x ∞ = anything you like! Intrigued? Read on…
LONG ANSWER: the question seems absurd: after all, zero multiplied by anything is zero, yet any multiple of infinity is always infinity. But 0 x ∞ cannot be both zero and infinity, can it?
Infinity doesn’t behave in the same way as other numbers; treating it as such quickly leads to a paradox:
∞ + 1 = ∞ (because ∞ is the biggest number, so adding one cannot make it any bigger).
Now subtract ∞ from both sides and we get:
0 = 1
Multiply both sides by any number you like, for instance 57:
0=57
By the same logic, all numbers are equal to zero, and so all numbers are equal.
Oh dear!
To make sense of it all we need the integral calculus (or just integration for short).
At GCSE: we learn the formulae for the areas of standard shapes like rectangles, circles and trapeziums.
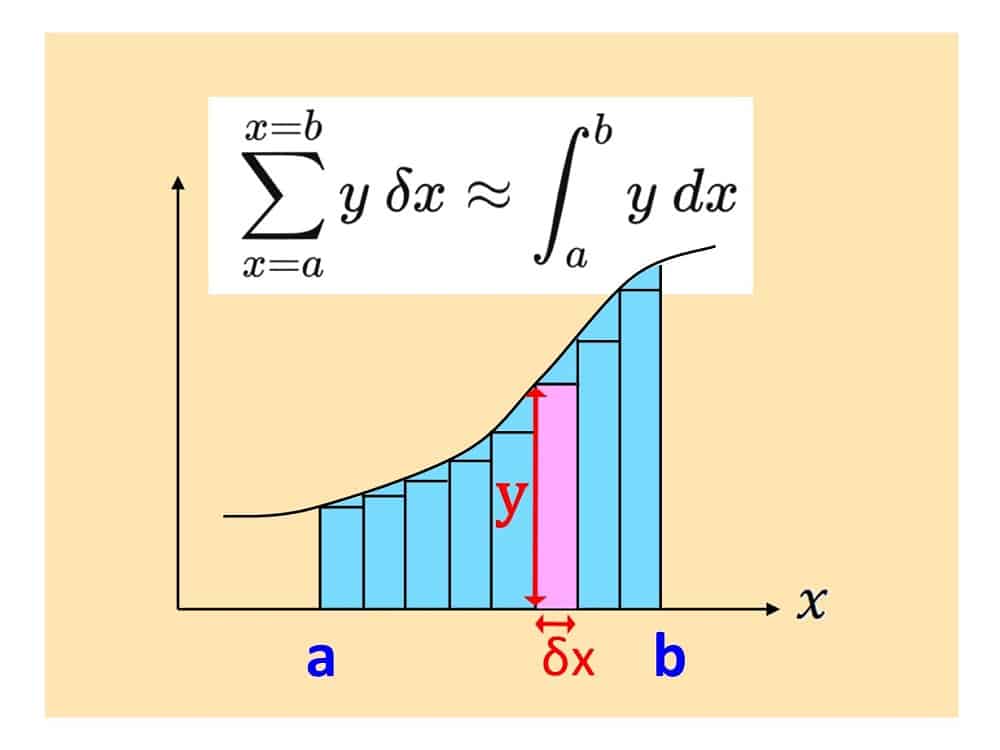
At A-level: we would also like the area of curved shapes. Integration finds the area under any curve by slicing it into tall thin sections (pictured) and adding up the areas of the sections. In the image we use n=8 rectangles to approximate the area under the curve (shaded blue). The more slices we use, the better the fit of these approximating rectangles to the (blue) area under the curve. Each rectangle has area $y$ (height) x $δx$ (width “delta ex”). The $\Sigma$ (“Sigma“) tells us to Sum these areas between $x=a$ and $x=b$.
Where do 0 and ∞ fit in? But the larger the number of slices n (say “as n tends to infinity”) the smaller the area of each rectangle (say each area “tends to zero”). As n is allowed to get arbitrarily enormous, the area under the curve (shaded blue) is precisely equal to 0 x ∞. This technique, invented in 1600’s, is what we call integration. Since the area under the curve can of course be any size, this means that 0 x ∞ = any number you like.
Beyond A-level: a University maths course puts these ideas on a firm footing by defining very precisely what is meant by a limit.