- All
- A-level
- Further
- Geometry
- words
- GCSE
- Videos
- Calculus
- Number
- Puzzles
- statistics
- Mathematicians
- Calculator
- mechanics
TOP FIVE MATHEMATICAL SPIRALS
RECOMMENDED LEVEL: A-level 5) ARCHIMEDEAN SPIRAL: the spiral you see if you roll up a carpet and look side-on. Constant separation distance between each coil. See my video of how to draw one here or
CIRCLE THEOREMS
IN THIS VIDEO: all eight Circle Theorems needed for GCSE maths demonstrated and explained. NOTE: students of IGCSE ("International GCSE") also need to know the Intersecting Chords Theorem (not covered in this video).
WHAT SHAPE OF CYLINDER IS BEST?
THE TIN OF TUNA ON THE LEFT: is the traditional shape: quite wide and not very tall. I was intrigued to see recently (2024) that one producer of tuna (can on the right!) has recently
KEY DIFFERENCES BETWEEN GCSE MATHS AND A-LEVEL MATHS?
Thinking of taking A-level maths? Here are some key differences you'll find from the style of GCSE maths, all designed to make our life easier not harder: 1) EMBRACE THE ALGEBRA! Maths is ultimately about
WHAT’S THE POINT OF A “RECIPROCAL”?
A QUICK REMINDER: The reciprocal of a number is: either: turn it upside down or (equivalently): one divided by that number. So the reciprocal of $\frac{2}{3}$ is $\frac{3}{2} = 1.5$ and the reciprocal of $5$
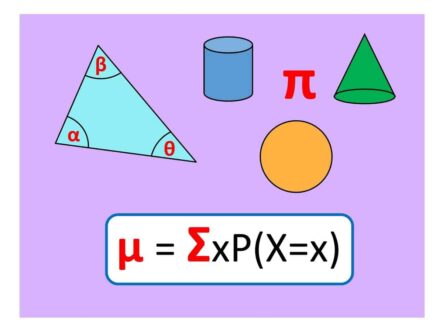
WHAT’S THE POINT OF USING GREEK LETTERS IN MATHS?
AT GCSE: introducing Greek letters (α, β, γ, δ, ...) leaves the more familiar Roman letters (a, b, c, d, ...) free to represent other quantities and unknowns. To start with, here are two Greek
WHAT’S THE POINT OF CHI-SQUARED GOODNESS OF FIT TEST?
TARGET AUDIENCE: A-level statistics or A-level Further Maths. A Real World example of a chi-squared test in action follows: this sort of test is extremely useful in a huge range of real-world scenarios!At our board
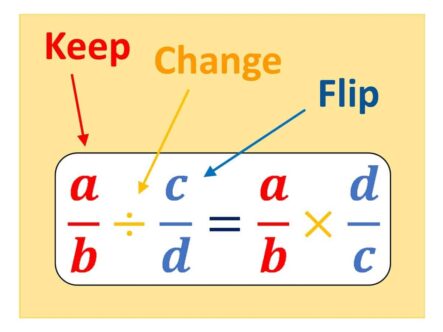
WHY DO YOU “KEEP, CHANGE, FLIP” WHEN DIVIDING FRACTIONS?
Aimed at: KS3, GCSE and A-level First we will see why it seems to make sense that you can divide by a fraction by simply flipping it upside down and multiplying; then we will prove
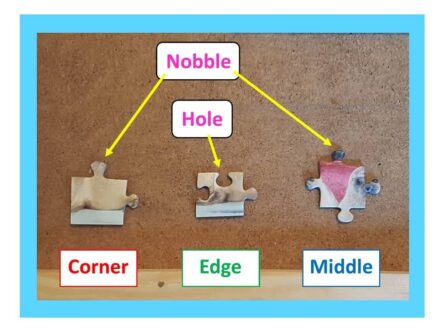
HOW MUCH HARDER IS A 2000 PIECE JIGSAW THAN A 1000 PIECE JIGSAW?
First of all, it's easy to see that a 2000 piece jigsaw is more than twice as hard as a 1000 piece jigsaw. To see why: imagine having two 1000 piece jigsaws that are of
Quote of the week: DIFFERENTIATION IS A SKILL. INTEGRATION IS AN ART.
I was delighted to find this quote at the start of Seán M. Stewart's book "How to Integrate it".One of the main differences between GCSE and A-level maths is the introduction of calculus. This branch
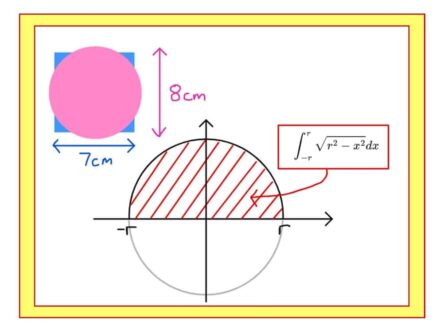
WHAT’S THE POINT OF INTEGRATION BY SUBSTITUTION?
A PUZZLE: which of these shapes is larger: a square of side 7cm or a circle or diameter 8cm? Well that's easy to answer if you know that the area of a circle is $A=\pi
TOP TEN SAMPLING METHODS
A quick reminder: if there are 1200 students at our school, it would be very time-consuming (if not impossible) to interview them all for your Sociology project. Here the population is everyone at the school,
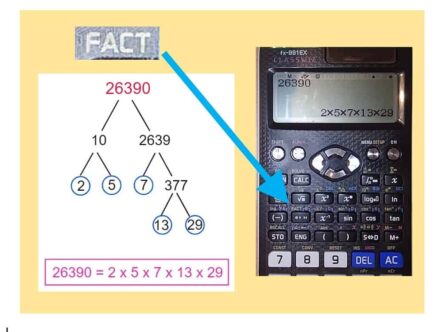
PRODUCT OF PRIME FACTORS – A CALCULATOR SHORTCUT!
Expressing a positive integer (whole number) as the product of prime factors is a bit like dismantling a machine to see what it's made of. Let's try it with 26390. Drawing a Prime Factor Tree
WHAT IS THE “AVERAGE” IN MATHS?
An average is simply a way of picking out a typical value from a set of objects (usually numbers). There are infinitely many different ways to pick a "typical value", but here are some of
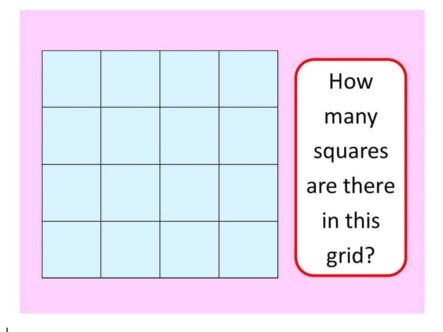
HOW MANY SQUARES ARE THERE IN THIS GRID?
Before we see the quickest way to answer the question (scroll down if you are an expert!), let’s see some different possible approaches: GCSE APPROACH: There are 16 little squares.There is the one large square
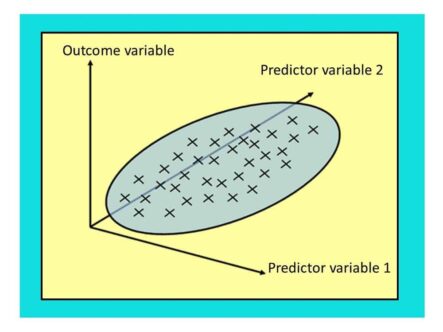
Regression: lines (and planes) of best fit.
Let's suppose we have some data for height and weight of some adult humans. We suspect the weight depends on the height - so taller people tend to weigh more than shorter. How can we
What does “MATH ERROR” mean?
SHORT ANSWER: this means you have just asked the calculator to do a sum it doesn't like. The three most common reasons for getting this error message are: 1) you have tried to divide by
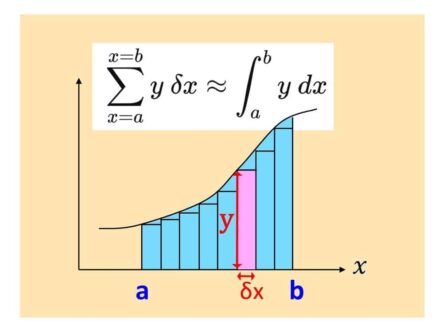
WHAT’S ZERO TIMES BY INFINITY?
SHORT ANSWER: 0 x ∞ = anything you like! Intrigued? Read on... LONG ANSWER: the question seems absurd: after all, zero multiplied by anything is zero, yet any multiple of infinity is always infinity. But
THE GREATEST MISTAKE IN THE HISTORY OF MATHS:
This must surely be the exclusion of women from maths for most of our history, due to mathematics (and academia in general) being seen as an unsuitable activity or as simply “too hard” for women.
USING MATHS TO CHECK WORLD RECORD ATTEMPTS: PETE’S DIABOLO HIGH THROW
My friend Pete can throw a diabolo ridiculously high - check out this video of him in action! Pete thinks his throw is higher than the “official” world record of 23.92metres so asked me if
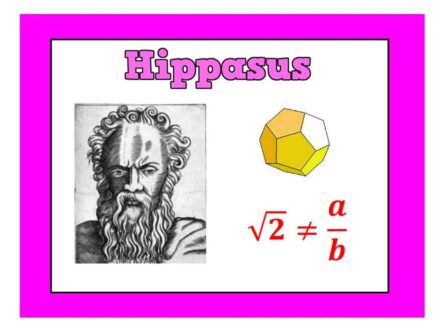
HIPPASUS
HIPPASUS: was an Italian born mathematician who lived around 500BC. Legend has it that Hippasus was drowned at sea after daring to suggest that some numbers cannot be written as one whole number divided by
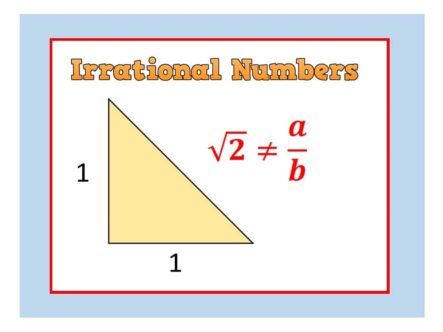
Strange but True: IRRATIONAL NUMBERS
The first numbers we discover in childhood are the Natural Numbers: 1, 2, 3, … Next come the Integers (whole numbers) – which also include Zero and the negatives: ... -3, -2, -1, 0, 1,
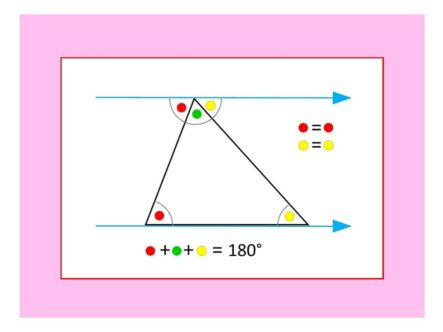
WHY THE ANGLES IN A TRIANGLE ADD TO 180°
Given any triangle: Rotate so that the longest side lies horizontally along the base. Extend the base, and draw a parallel line going through the uppermost corner (these two lines are shown in light blue).
What’s special about ZERO?
(or: Much ado about Nothing)
Zero doesn’t actually exist. Think about it: by definition it isn’t anything, it’s nothing!! Even so, here are 5 facts every mathematician should know about Zero:
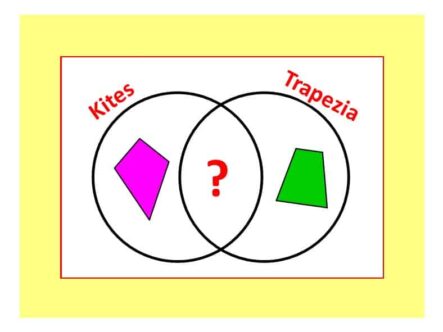
PUZZLE OF THE WEEK
What shape goes in the intersection of this Venn Diagram?
Read on for the answer:
HOW DO GRADIENTS WORK?
Here I am at the World's Steepest Road in Harlech, North Wales. The road sign indicates an almighty 40% - but how is this measured? ON ROADS: The 40% means that however far you travel
5 WAYS TO TYPE SYMBOLS π λ √∫≤∑≈
not to mention $\frac{e^{-t}}{y^3+1}$ To type Mathematical Symbols on your PC: 1) USE WINDOWS EMOJIS: To type ⅷ∀√∛∞∑²³ⁿ∃∞∫≈≡≥ and many more. Simply press windows key together with . to bring up the emoji keyboard, then
WHICH ARE BETTER: FRACTIONS OR DECIMALS?
DECIMALS ARE WAAAY BETTER THAN FRACTIONS: most GCSE students prefer decimals because they allow you to compare the sizes of two numbers at a glance! For instance, which is bigger out of $\frac{2}{5}$ and $\frac{3}{7}$?
QUOTE OF THE WEEK: “God Made the Integers. All Else is the Work of Man”
... or so thought Leopold Kronecker (1823-1891) in his famous quote. WHY KRONECKER WAS WRONG: the integers (whole numbers) include the Positive Integers or "counting numbers" 1, 2, 3, 4 and so on: easy for
HYPOTHESIS TESTS
In statistics, these wonderful techniques allow us to use some data that we have collected to make predictions and conclusions about the real world. AN EXAMPLE: Amy and Bill are playing snakes and ladders, but
FACTORIALS!
Factorials are so cool that the notation is: AN EXCLAMATION MARK!!!! The exclamation mark means something very specific in maths. It's great to be impressed with numbers, but please do not put an exclamation mark
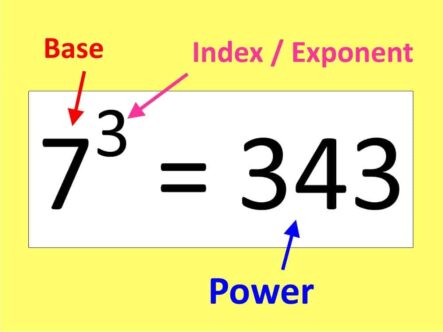
WORD OF THE WEEK: INDEX
INDEX (plural indices): you can see these in expressions like $5^2 = 25$. The 5 is called the BASE, the 2 is called the EXPONENT or INDEX, and the 25 is called a power (in
GEOMETRY PUZZLE: WHAT SHAPE DO YOU SEE?
TRICKY TILINGS:
Tiling stores are like treasure troves of geometrical amusement. Here’s a photo I took yesterday. The puzzle is simply: what shape(s) do you see?
ANSWER: ....
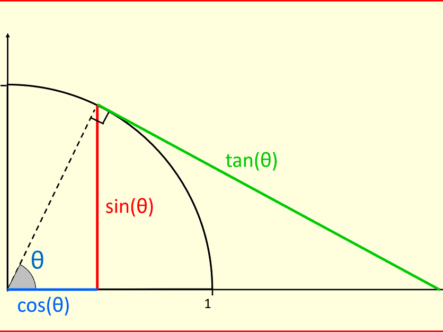
WORD OF THE WEEK: TRIGONOMETRY
TRIGONOMETRY is the branch of maths to do with sin, cos and tan (find them on your calculator). Literally it means “measuring triangles” – so you can use these three functions to find unknown lengths
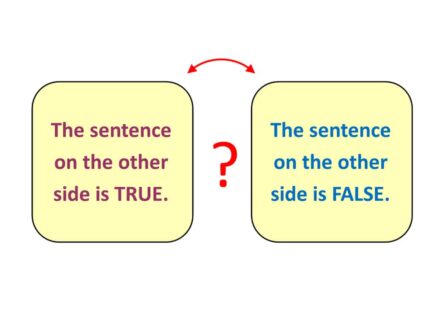
CURIOUS LOGIC
CURIOUS LOGIC: on one side of a postcard are written the words “the sentence on the other side is true”. You turn over the card to see the words “the sentence on the other side is false”. Which of the two sentences, if either, is the true statement? - Head over to the Blog page to find out the answer.