Strange but True: IRRATIONAL NUMBERS

The first numbers we discover in childhood are the Natural Numbers: 1, 2, 3, …

Next come the Integers (whole numbers) – which also include Zero and the negatives: … -3, -2, -1, 0, 1, 2, 3, …

Next up: it’s fractions such as:

0.5, 2.90909… , $-\Large{5}\frac{7}{8}$

Numbers like these are said to be Rational because they can be made by dividing two integers. The three fractions above are $1\div 2 = \frac{1}{2}$, $32 \div 11 = \frac{32}{11}$ and $-47\div 8 = \frac{47}{8}$

These rational fractions are infinitely dense on the number line. So for instance there are infinitely many fractions between 1 and 2. There are also infinitely many fractions between say 1.47 and 1.48. Because the rationals are so dense on the number line it seems bizarre to discover that there are some numbers in between the integers that cannot be made by dividing two integers! Such numbers are called Irrational – a word that is also commonly used (not in maths) to describe something that doesn’t seem to make a lot of sense!

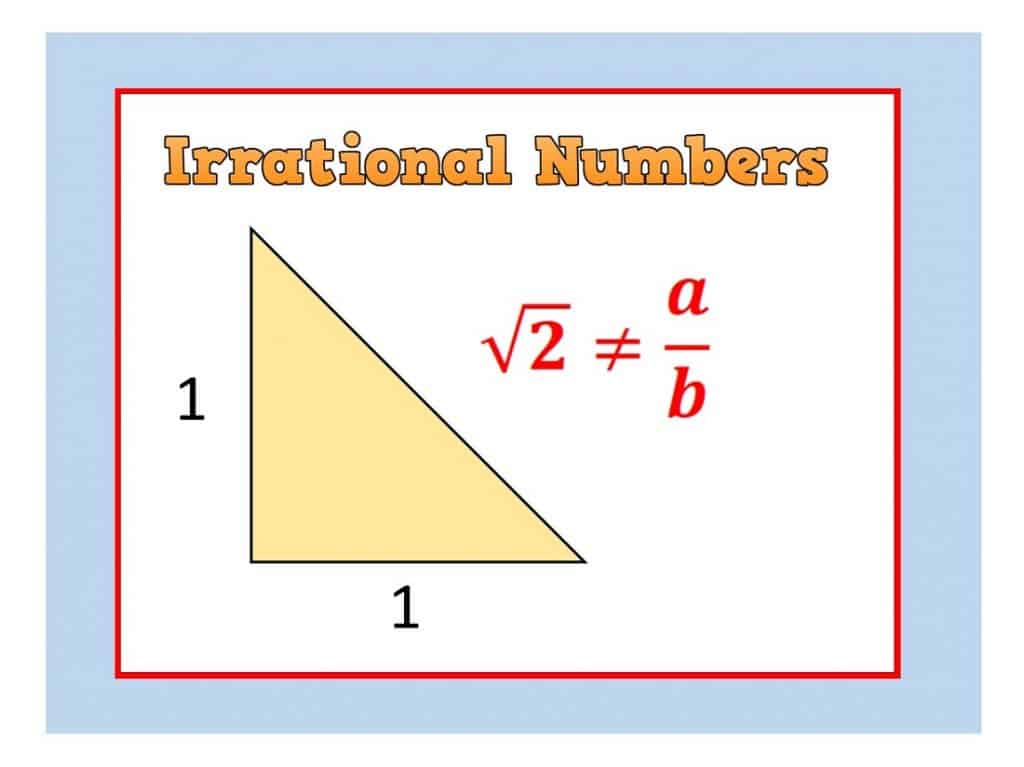
Take this triangle, made from a unit square (a square whose side is of length one unit) chopped in half corner to corner. The diagonal clearly has a measurable length, and Pythagoras Theorem tells us that the length is $\sqrt{2}$. Amazingly, it turns out that $\sqrt{2}$ cannot be written as the quotient of two integers ( i.e. as one divided by the other).

AT GCSE: we introduce irrational numbers by looking at surds. These are irrational square roots such as $\sqrt{2}$, $\sqrt{3}$ and $\sqrt 5$

AT A-LEVEL: we prove that $\sqrt{2}$ is irrational, and that when it’s written as a decimal, its expansion will go on forever without ever repeating

$\sqrt{2} = 1.414213562373095048 … $

If the idea that a number can go on forever without ever repeating seems a little weird then join the club: legend has it that Hippasus of Greece (c.500BC) was murdered just for suggesting this might be true.

BEYOND A-LEVEL: at University you might prove that numbers such as π and e are also irrational. Another famous and surprising result proves that, not only do irrational numbers exist, but they are in some sense even more numerous than the rational numbers.