PRODUCT OF PRIME FACTORS – A CALCULATOR SHORTCUT!

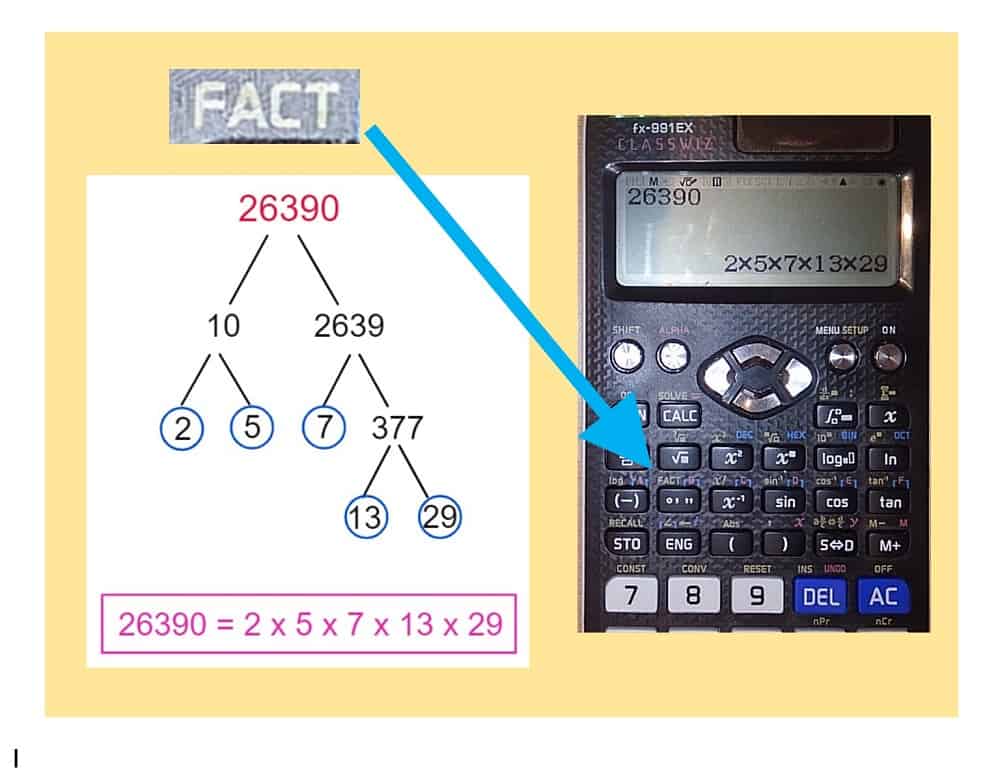
Expressing a positive integer (whole number) as the product of prime factors is a bit like dismantling a machine to see what it’s made of. Let’s try it with 26390. Drawing a Prime Factor Tree will take a while – but fortunately the calculator can do the hard work for us! Type in 26390, press = , then look for the FACT button – on my Casio fx you press shift first to get the button’s second function. Voilà: 26390 = 2x5x7x13x29.

AT GCSE: you are still required to “show your working” by drawing the prime factor tree, but it doesn’t hurt to use the calculator to check your answer.

THE FUNDAMENTAL THEOREM OF ARITHMETIC: This grandly named result says that it doesn’t matter in which order you split an integer apart, you will always get the same answer. In the case of our example 26390, many students would start by halving it: 26390 = 2×13195, but I think a better idea is to note that it ends with a zero, so 26390 = 10 x 2693 – this approach makes the numbers smaller more quickly. It’s difficult to see what goes into 2639. Two doesn’t, neither does 3 or 5, so let’s try 7: yes, it works! And so on until you are left with just primes.

WHAT’S THE POINT?: Expressing numbers as the product of their prime factors is the easiest way to find the LCM (Lowest Common Multiple) of two or more numbers.

The LCM of, say, 15 and 24 would be needed to find the lowest common denominator so you can add $\dfrac{7}{15} + \dfrac{5}{24}$.

You’d also need the LCM to answer this question:

Paula can run a lap of a running track in 15 minutes. Mohammed can run a lap in 24 minutes. If they start together at the same time, after how many minutes will they next be back at the starting line together?? The answer is of course the LCM of 15 and 24.

AT UNIVERSITY LEVEL (read on if you dare!): the Fundamental Theorem isn’t at all obvious and I’m still impressed by this result every time I see it. Proving it is very tough, but I can give you a flavour of how it works here, using proof by contradiction:

STEP 1: start by assuming the opposite of what we’re trying to prove: so assume that there is a number which can be factorised in two different ways. Let’s call such a number an counterexample to the fundamental theorem. We’re hoping that this assumption will lead to a contradiction, proving that our assumption was incorrect. The proof will then be complete.
STEP 2: if there is an counterexample then there must be a smallest one: we call this the minimal criminal: the smallest number which can be factorised into primes in two different ways. Call this number $x$.
STEP 3: by assumption we can write $x$ in algebraic form in two different ways: $x = p_1p_2…p_m = q_1q_2…q_n$.
STEP 4: observe that all the p’s must be different to all the q’s – because if for instance $p_1 = q_1$ then we could divide both expressions by this prime to get a smaller counterexample, contradicting the assumption that x is the smallest one.
STEP 5 (the tricky bit!): use our two expressions to construct a counterexample that’s smaller than x, contradicting our assumption that x is the minimal criminal (smallest exception).
STEP 6: our assumption that a counterexample existed has led to a contradiction, and so the assumption must have been incorrect. Therefore there is no counterexample, so the Fundamental Theorem is true!