Aimed at: KS3, GCSE and A-level
First we will see why it seems to make sense that you can divide by a fraction by simply flipping it upside down and multiplying; then we will prove it works.
INTUITIVELY:
Let’s see if we can find a rule for dividing by $\frac{1}{2}$.
The $\frac{1}{2}$ times table goes like this: $\frac{1}{2}, 1, 1\frac{1}{2}, 2, 2\frac{1}{2}, 3, …$. Therefore:
$1\div \frac{1}{2} = 2$ because $\frac{1}{2}$ goes into one two times.
$2\div \frac{1}{2} = 4$ because $\frac{1}{2}$ goes into two four times.
$3\div \frac{1}{2} = 6$ because $\frac{1}{2}$ goes into three six times.
Hmm, it’s looking like dividing by $\frac{1}{2}$ is the same as multiplying by 2. This suggests the rule that $\div \frac{a}{b}$ is the same as $\times \frac{b}{a}$
Now let’s prove it!
THE PROOF:
As with most mathematical proofs, algebra is the language that lets us deal with all cases at once: in this case we will divide $\frac{a}{b} \div \frac{c}{d}$ rather than choosing specific numbers.
We start by recalling the following:
If you multiply the top and bottom of a fraction by the same number, you get an equivalent fraction.
And if you divide the top and bottom of a fraction by the same number, you again get an equivalent fraction (this means we can “cancel” any multiplier on the numerator of a fraction with the same multiplier on the denominator).
Now then:
$\frac{a}{b} \div \frac{c}{d}$
$ = \Large{\frac{\frac{a}{b}}{\frac{c}{d}}}$
Now we multiply top and bottom by $bd$ to clear the “fractions within fractions” – we can do this and still have an equivalent fraction:
$ = \Large{\frac{\frac{a}{b} \times bd}{\frac{c}{d} \times bd}}$
$ = \large{\frac{a\times d}{b \times c}}$ (because the b’s cancel on top, and the d’s cancel on the denominator)
$ = \large{\frac{a}{b} \times \frac{d}{c}}$
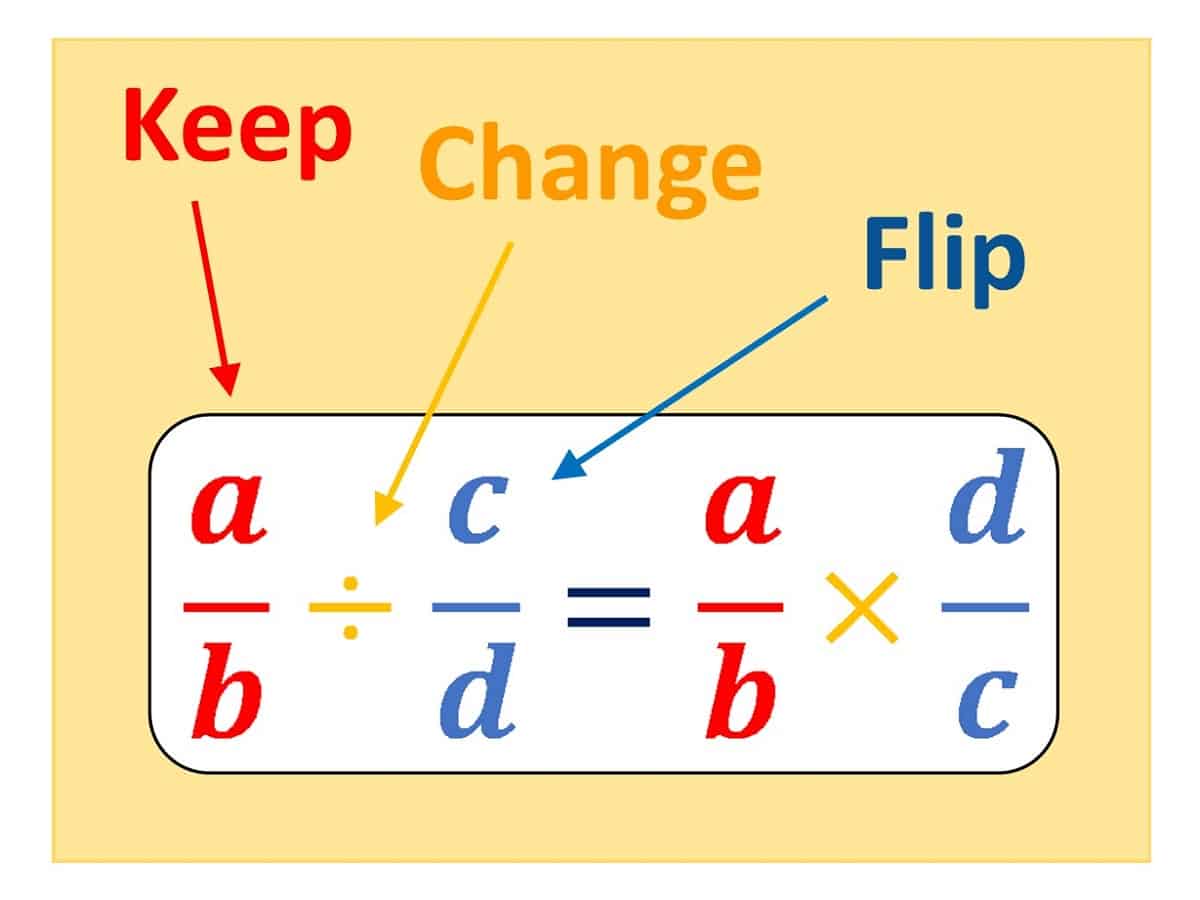
so it is as if we had simply kept the first fraction, changed $\div$ to $\times$, and flipped the second fraction: KEEP, FLIP, CHANGE.
Magic!