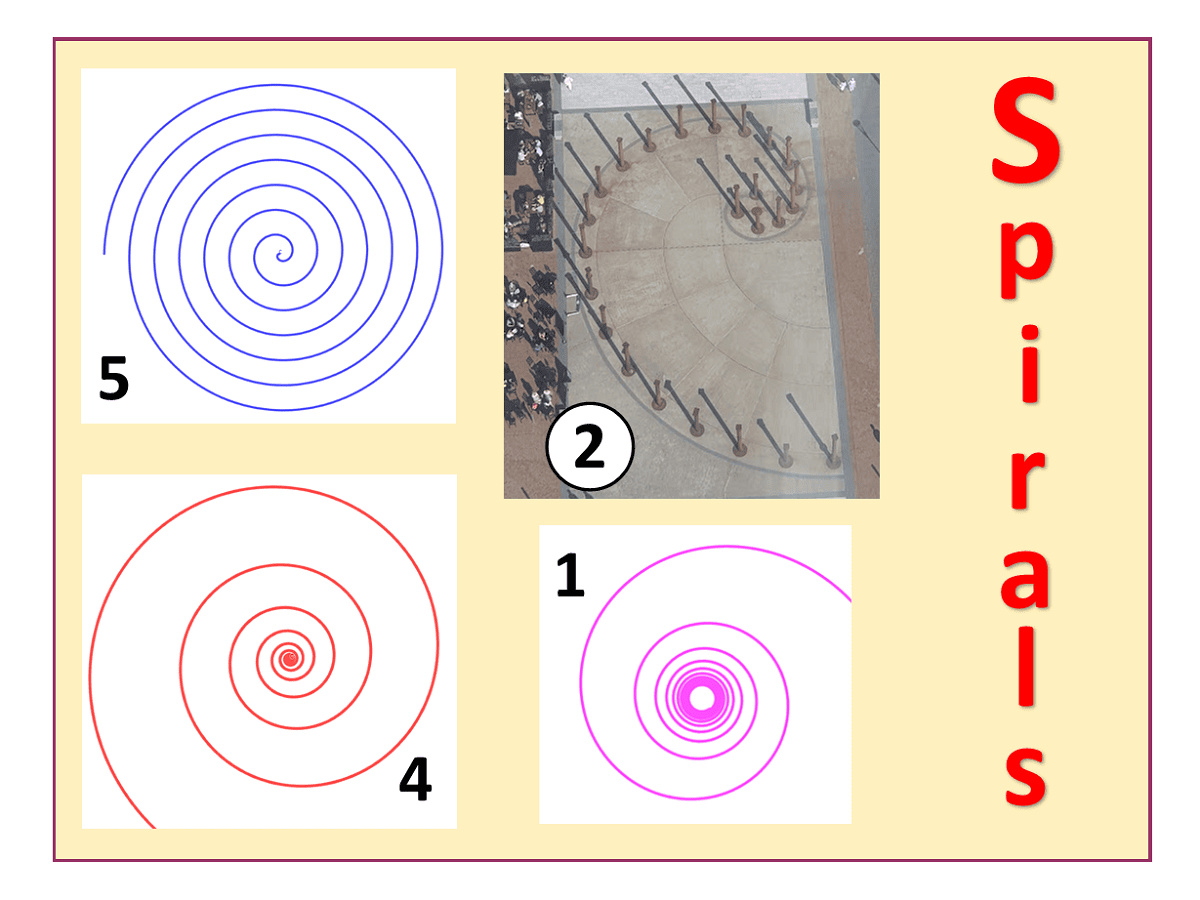
RECOMMENDED LEVEL: A-level
5) ARCHIMEDEAN SPIRAL: the spiral you see if you roll up a carpet and look side-on. Constant separation distance between each coil. See my video of how to draw one here or use your favourite free graph sketching software (e.g Geogebra or Desmos). For A-level Further Maths students: the polar equation is $r=aθ$ where the parameter a makes the (constant) separation distance between each coil larger or smaller.
4) LOGARITHMIC SPIRAL: a spiral in which the distance from the central point increases more and more quickly as the angle of rotation increases – meaning that the separation distance between successive turns increase in geometric progression: in A-level maths we learn that a geometric sequence occurs when the term-to-term rule is to keep multiplying by the same number. This is different to an Archimedean spiral, in which the distance between coils stays constant. The logarithmic spiral is often seen in nature, for instance in the arms of some spiral galaxies, or in the approach of an insect to a light source. A-level Further Maths: the polar equation is $r=ae^{kθ}$ where the parameter k determines the separation distance factor between successive coils.
3) GOLDEN SPIRAL: a type of logarithmic spiral in which the radius increases by a factor of the golden ratio “phi”
$\Large{\phi = \frac{1+\sqrt{5}}{2}}$
per quarter turn. Why is that even a thing?!? Despite the claims of some mystics, the Golden Spiral is unremarkable except for one fact: it is fun and easy to make one approximately by drawing a Fibonacci Spiral (see next!). See my video of how to draw one here on read on for a description.
2) FIBONACCI SPIRAL: an easy-to-draw spiral that approximates a Golden Spiral using quarter-circle arcs inscribed in squares derived from the Fibonacci Sequence. Confused? Then read on: the construction is easy to do and really fun!
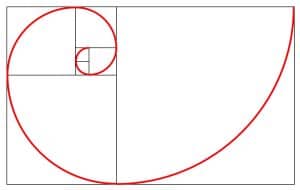
Using squared paper, draw squares of side length 1, 1, 2, 3, 5, 8, 13, … and so on, arranging the squares in a spiral pattern (see picture!) in such a way that each square is as long as the sum of the previous two squares. These lengths are the famous Fibonacci Sequence of numbers (to find each number, add the previous two terms). Now draw a quarter circle inside each square, as shown, in a continuous “Fibonacci Spiral”. The ratio of successive Fibonacci numbers gets closer and closer to the golden ration phi (see Golden Spiral) – which is how we know that the Fib Spiral is a good approximation to the Golden Spiral. Pictured at the start is a huge Fib Spiral sculpture that I spotted from 100m up in the air on a recent trip to Brighton (photographed from the Brighton i360 observation tower). A-level Further Maths: the value of the parameter k in the logarithmic spiral equation is $k=\frac{ln2}{π/2}$. Check that this ensures a growth factor of φ between successive coils.
1) HYPERBOLIC SPIRAL: so cool and my current favourite! This one spirals inwards towards the centre rather than outwards away from the centre, and is the spiral shape that you see if standing at the bottom of a spiral staircase looking straight up. The polar equation is $\large{r=\frac{a}{θ}}$ but you will need to draw many turns to see the effect (suggest use $0\leq θ \leq 10\pi$).
WANT TO KNOW MORE? Check out my video on Archimedean and Golden Spirals.