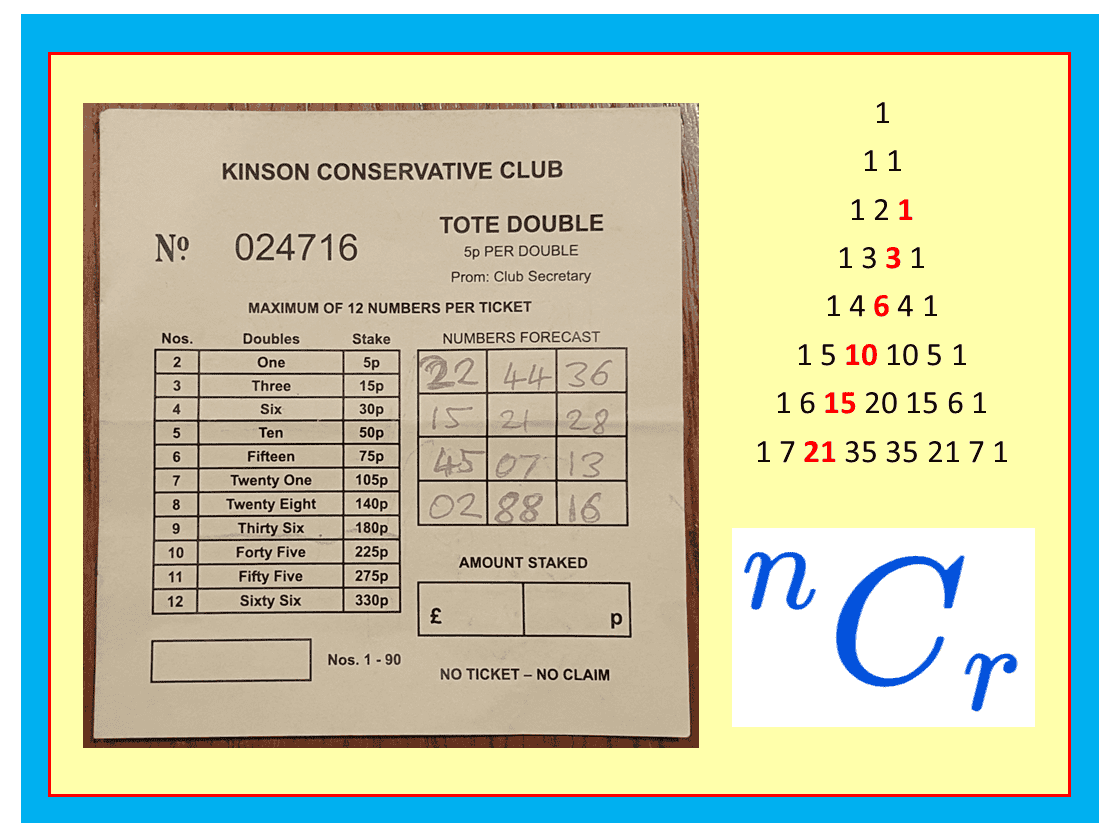
I’ve just returned from an evening at the Kinson Social Club, where I was invited to take part in a TOTE DOUBLE competition. I’m not normally a betting man: because a bet usually means that on average you put in more money than you expect to win, meaning that on average you lose money. But this evening I felt obliged to take part. I dutifully paid my £3.30, having no idea of the rules, and was invited to choose up to twelve “lucky” (?) numbers. Here’s my betting card: what on earth do all these numbers mean?
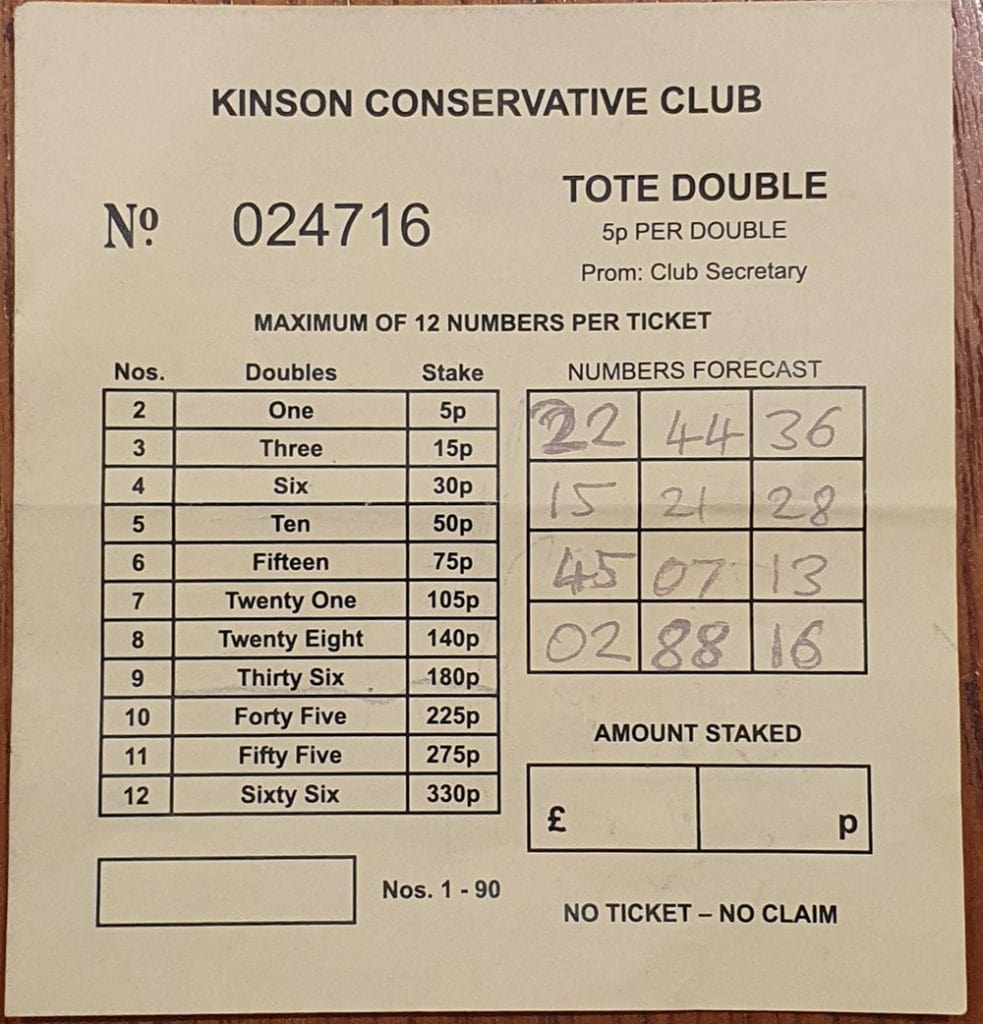
THE FIRST COLUMN: I later discovered that you could choose between 2 and 12 “lucky” numbers (between 1 and 90). The other players on my table chose their birthday or other significant numbers; being put on the spot and not knowing the rules I opted for a mixture of multiples of my house number (can you work out from the photo what house number I live at?), square, prime and triangular numbers. I included 36 because it’s both square and triangular ($36=6^2$ and also $36=1+2+3+4+5+6+7+8$)! Later in the evening, some numbers would be randomly chosen. The first player to have two of their “lucky” numbers read out should shout out “YES I’M THE WINNER!!” or something similar. Should this be two or more players, they would share the winnings. Not knowing what I was doing, I decided to “go big” and pay £3.30 for the privilege of choosing the maximum possible twelve numbers!
TOTE BETTING: refers to the notion that all the money spent by those taking part is added to the same “pool”. The winner (or winners) share a percentage of that pool (in our case I’m guessing it was perhaps 85%, the remaining 15% going to the club so that they make a little profit in exchange for running the competition). In tonight’s competition you needed to have selected two correct numbers, hence “tote double“.
THE SECOND COLUMN: this fascinated me: I quickly noticed a load of triangular numbers!! After seeing later how the game worked, the magic became clear, and I was able to amuse my table by having them ready out the first number, while I responded with the number in the second column. How so?
As an example, let’s take the row beginning “7 | Twenty One”. The idea here is that if you pay to choose 7 numbers than you have 21 different ways of winning. To work this out: if you choose 7 numbers then there are $^7C_2=21$ different pairs of numbers that might be the winning combination.
COMBINATIONS: $^7C_2$ is the number of ways of choosing 2 objects from 7 if the order doesn’t matter. Imagine you have 7 different coloured pens and you are asked to choose two of them; in how many ways can you do this? The answer is $^7C_2$ which turns out to be $21$. The formula is:
$^nC_r=\frac{n!}{r!(n-r)!}$
where $n!$ (pronounced “n factorial”) is the product of the first n integers $1\times 2 \times 3 \times …$ all the way up to $\times n$. A really easy way of calculating $^nC_2$ is to work out $\frac{n(n-1)}{2}$ so for instance $^7C_2=\frac{7 \times 6}{1 \times 2}=21$ and (moving to the next row) $^8C_2=\frac{8 \times 7}{1 \times 2}=28$. Using this shortcut I was easily able to calculate the numbers in the second row from the numbers on the first row.
THE THIRD COLUMN: this merely tells you how much you should pay for the privilege of choosing this number of possible winning combinations. At 5p per possible win, this number is simply 5p times the number from column 2. In my case I chose 12 numbers, giving m $^{12}C_2=66$ possible ways to win, so I paid $66 \times 5p = £3.30$ as my entry fee to the competition.
PASCAL’S TRIANGLE: you may have noticed that the numbers in the middle column are also the triangular numbers, appearing in the third diagonal of Pascal’s Triangle (see the opening image).
SO WHAT HAPPENED?: the first three numbers read out included just one of mine (unsurprisingly, because the probability of this happening is $\frac{12}{90} \times \frac{78}{89} \times \frac{77}{88} \times 6 \approx 0.613 = 61.3$%). Two other players shared the prize: they went home with approx £40 each, and I went home smiling at yet another occurrence of triangular number in the real world!