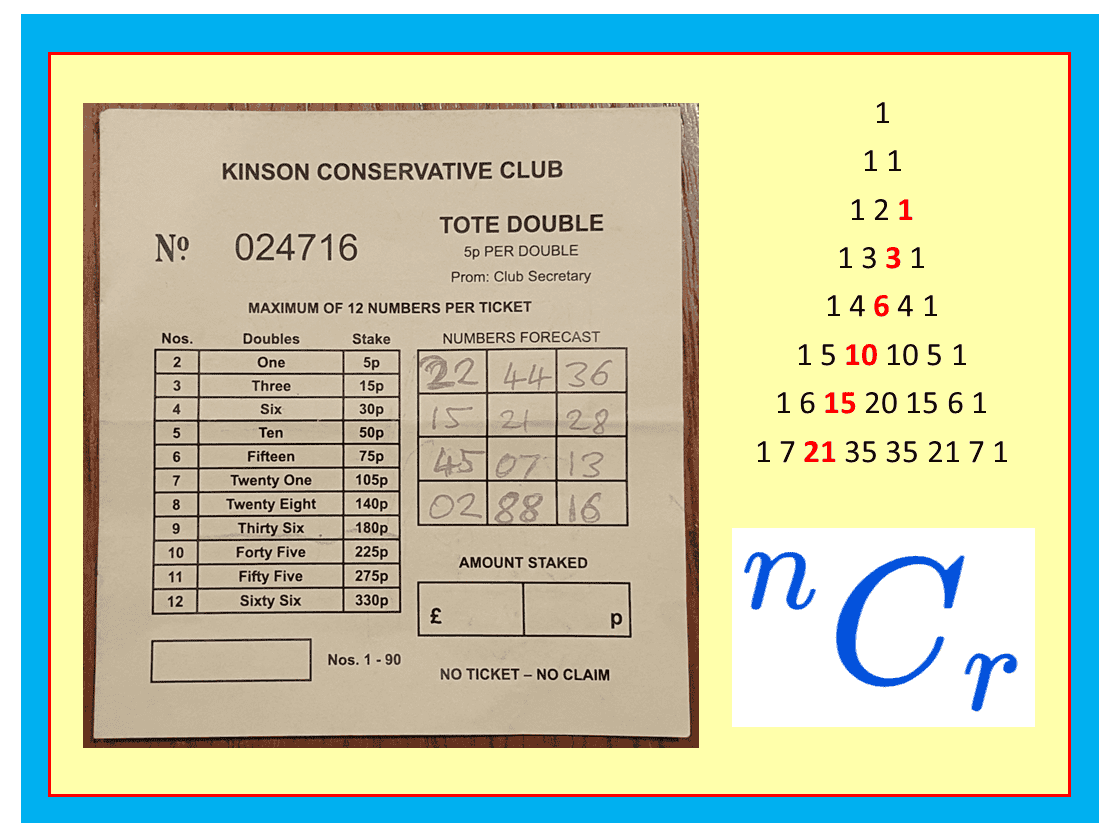
I’ve just returned from an evening at the Kinson Social Club, where I was invited to take part in a TOTE DOUBLE competition. I’m not normally a betting man: because a bet usually means that on average you put in more money than you expect to win, meaning that on average you lose money. But this evening I felt obliged to take part. I dutifully paid my £3.30, having no idea of the rules, and was invited to choose up to twelve “lucky” (?) numbers. Here’s my betting card: what on earth do all these numbers mean?
HOW FAST MUST THE BALL GO TO COMPLETE A LOOP THE LOOP?
Big Shout Out to the Bognor Regis Mini Golf in PO21 1TE. If you can visit: please do so and try this puzzle out for yourself!
So, how fast must Anastasia hit the golf ball so that it completes the loop-the-loop?
WHAT’S SPECIAL ABOUT THE NUMBER 2025?
or: Why is the square of the nth triangular number equal to the sum of the first n cubes?
SUGGESTED LEVEL: Further Maths A-level or anyone at any level if you love numbers!
Every New Year brings a new number for us all to wonder about: is this year a prime number? A square number? Something else?? As I write we are at the start of 2025 and the interest has been far higher than usual. So: why is 2025 such a very cool number?
SHORT ANSWER (read on if this makes no sense – I will explain!):
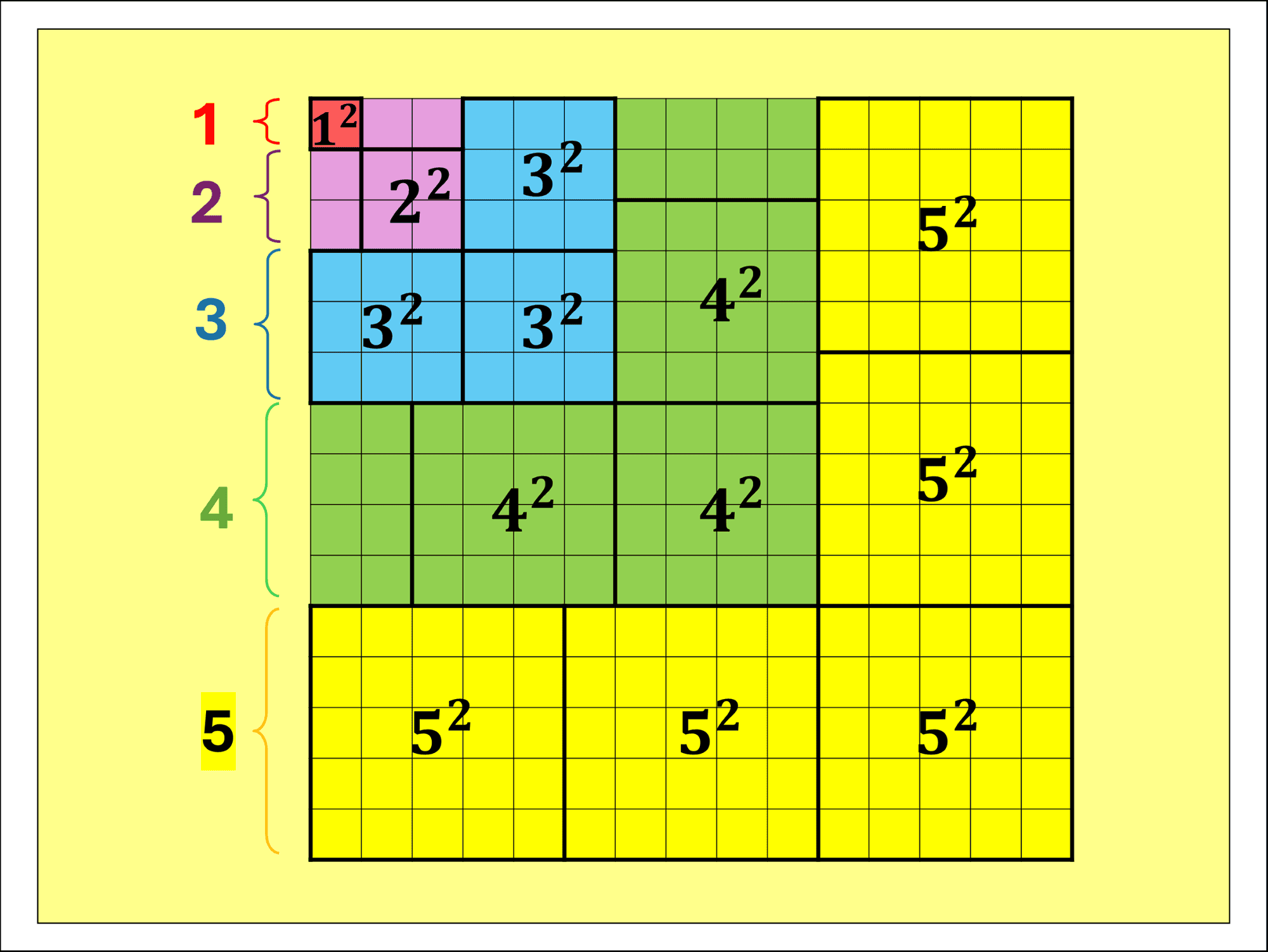
$2025=(1+2+3+4+5+6+7+8+9)^2=1^3+2^3+3^3+4^3+5^3+6^3+7^3+8^3+9^3$.
You can easily use a calculator to check that it’s true, but my maths brain really wants an intuitive way to see why this works – ideally using geometry (“shapes”) so I can picture the result!
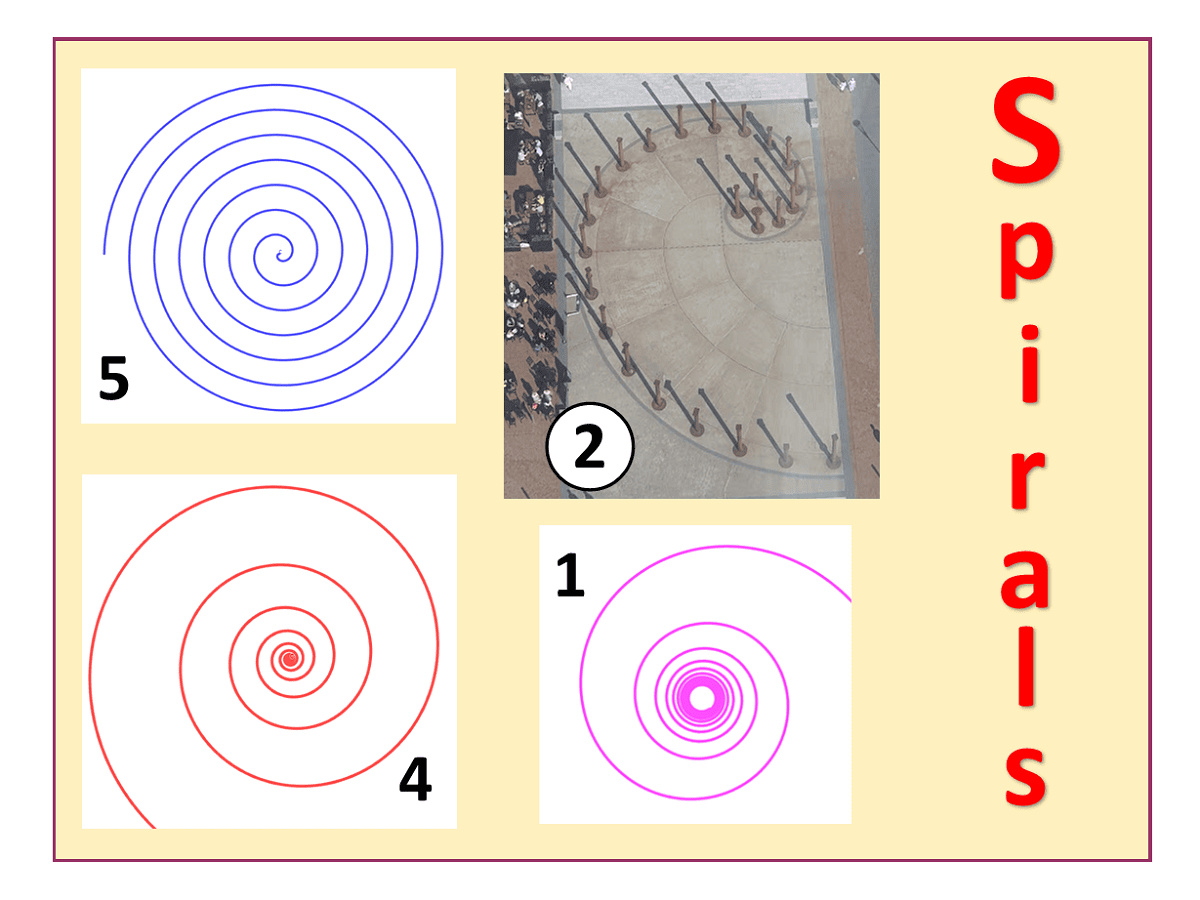
TOP FIVE MATHEMATICAL SPIRALS
RECOMMENDED LEVEL: A-level
5) ARCHIMEDEAN SPIRAL: the spiral you see if you roll up a carpet and look side-on. Constant separation distance between each coil. See my video of how to draw one here or use your favourite free graph sketching software (e.g Geogebra or Desmos). For A-level Further Maths students: the polar equation is $r=aθ$ where the parameter a makes the (constant) separation distance between each coil larger or smaller.
4) LOGARITHMIC SPIRAL: a spiral in which
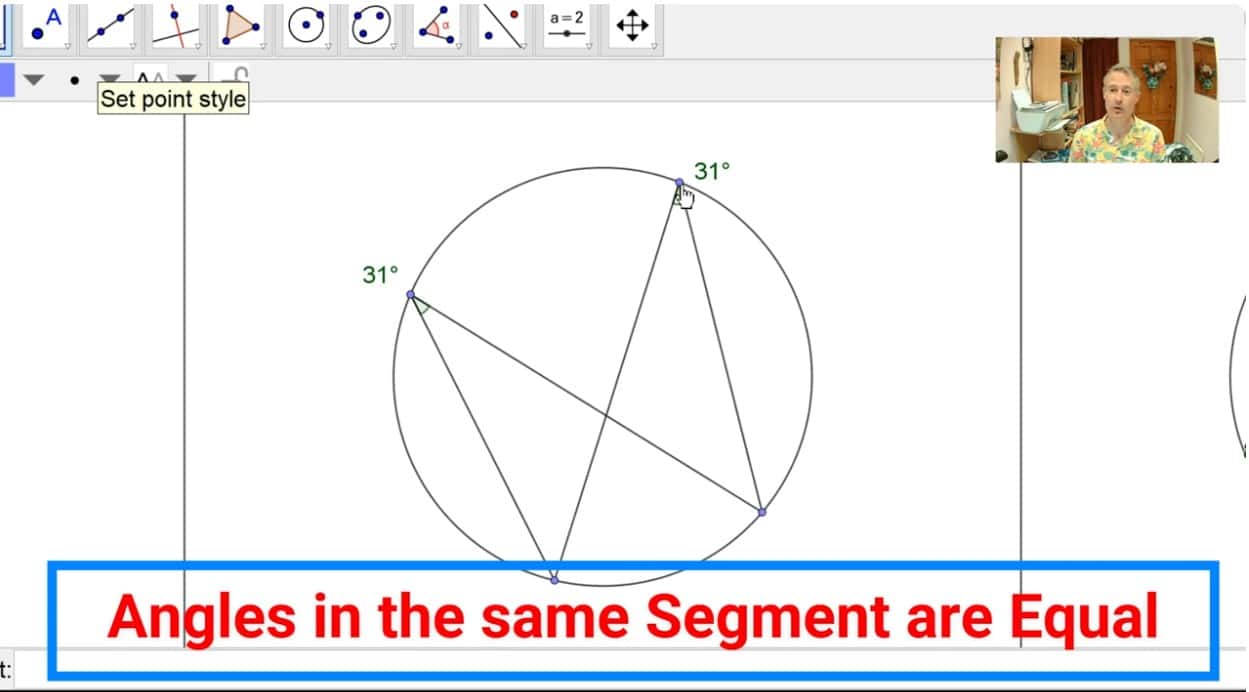
CIRCLE THEOREMS
IN THIS VIDEO: all eight Circle Theorems needed for GCSE maths demonstrated and explained. NOTE: students of IGCSE (“International GCSE”) also need to know the Intersecting Chords Theorem (not covered in this video).
WHAT SHAPE OF CYLINDER IS BEST?
THE TIN OF TUNA ON THE LEFT: is the traditional shape: quite wide and not very tall. I was intrigued to see recently (2024) that one producer of tuna (can on the right!) has recently
KEY DIFFERENCES BETWEEN GCSE MATHS AND A-LEVEL MATHS?
Thinking of taking A-level maths? Here are some key differences you’ll find from the style of GCSE maths, all designed to make our life easier not harder:
1) EMBRACE THE ALGEBRA!
Maths is ultimately about spotting patterns, and algebra is the language we use to write down patterns. A simple example: $A=l \times w$ is a formula to tell you how big a rectangle is. ANY rectangle. At GCSE, it is reasonable to develop clever tools to avoid having to use algebra; but at A-level, we must embrace algebra: it’s our friend and is there to make maths easier! An example:
WHAT’S THE POINT OF A “RECIPROCAL”?
A QUICK REMINDER:
The reciprocal of a number is:
either: turn it upside down
or (equivalently): one divided by that number.
So the reciprocal of $\frac{2}{3}$ is
WHAT’S THE POINT OF USING GREEK LETTERS IN MATHS?
AT GCSE: introducing Greek letters (α, β, γ, δ, …) leaves the more familiar Roman letters (a, b, c, d, …) free to represent other quantities and unknowns. To start with, here are two Greek
WHAT’S THE POINT OF CHI-SQUARED GOODNESS OF FIT TEST?
TARGET AUDIENCE: A-level statistics or A-level Further Maths. A Real World example of a chi-squared test in action follows: this sort of test is extremely useful in a huge range of real-world scenarios!At our board